New Long Distance Kill Shot Record (8,120 Feet / 2,706.67 Yards)

Here is something that has been in the news the last few days. A British Army
soldier by the name of Corporal Craig Harrison, of the Household Cavalry, set a
new record for the longest shot in combat. Twice. Cpl. Harrison fired two shots
at Taliban machine gunners in Afghanistan.They were confirmed via GPS to be 8,120 feet from Cpl. Harrison's position.
That is 1.54 miles. More than a mile and a half. To make it even more
astounding, the range was almost 3,000 feet beyond what is considered the
effective range of the weapon. At that range the bullet takes around 3 seconds
to reach the target.
The previous record was set in 2002 for a sniper kill at 7,972ft. That shot was
made by Canadian Corporal Rob Furlong, of Princess Patricia's Canadian Light
Infantry, who was using a .50BMG McMillan TAC-50 rifle.

Harrison accomplished this feat with the above pictured weapon, a L115A3 rifle.
The weapon is manufactured by Accuracy International in Britain and is
chambered in the .338 Lapua Magnum cartridge. This is significant because the
previous two shots that held the world record were with weapons chambered for
the .50 BMG. The .338 is a cartridge designed for accuracy and power beyond the
range of the older 7.62mm rifles. It has a much flatter trajectory, which makes
the complex trigonometry problem of finding the right arc to lob the bullet
onto the target much easier. It is one of several other "lighter"rifle rounds
like the .300 Win Mag., .416 Barrett, and .408 CheyTac that have
been designed with extreme long range shooting in mind. Of special importance
is the velocity past 1000 meters, the shape of its trajectory and how long the
cartridges stay supersonic.
The Accuracy International Arctic Warfare .338 is a bolt action, detachable
magazine-fed, precision rifle. The rifle is about 15 pounds, unloaded and
without optics. It can mount a variety of telescopic sights, laser designators,
and night vision or thermal sights. In British service, it usually mounts a
S&B 5-25x56mm day scope. The extra-large objective lens size of 56mm
gathers a lot of light, making shots possible in the dawn, dusk, or into the
shadows. The L115A3 can also mount a suppressor, helping to reduce the report
flash and dust from the powerful rifle. The barrel is free floated for
increased accuracy and is fluted for strength and cooling without excessive weight.
You don't get all that performance cheap though. News reports put the rifle at
around $25,000. But if you put it in the right hands and it can hit a sized
target from 4500 feet. More importantly, even at extreme range, the bullet
retains its power, hitting with more force than a .44 Magnum at 25 feet.
It was just unlucky for the Taliban that conditions were so good and we could
see them so clearly. We saw two insurgents running through its courtyard, one
in a black dishdasha, and one in green. They came forward carrying a PKM
machine gun, set it up and opened fire on the commanders wagon. The first round
hit a machine gunner in the stomach and killed him outright. He went straight
down and didn't move. The second insurgent grabbed the weapon and turned as my
second shot hit him in the side. He went down, too. They were both dead."
Cpl. Harrison had a memorable tour of duty, making the two impossible shots,
having a bullet deflect off his helmet, and surviving an IED blast that broke
both of his arms. He is reportedly healing well, and has returned to duty.
Corporal Harrison

CONGRATULATIONS ARE IN ORDER FOR CORPORAL HARRISON AND THE BRITS!!!
Here are the 9 greatest mechanical principles and
inventions, which show the greatness of the human mind.
Simple animation to explain complex principles:
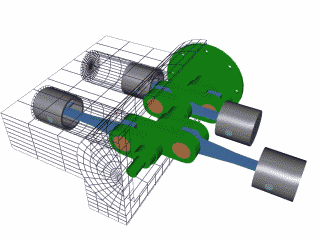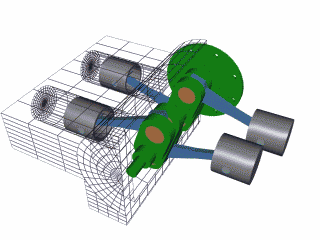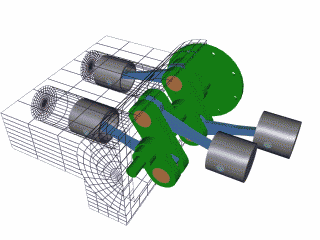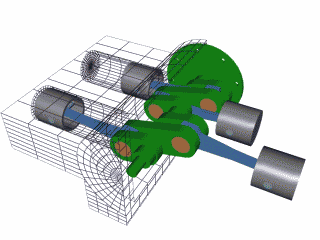
1: Aircraft Radial Engine
2: Oval Regulation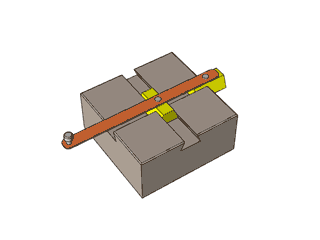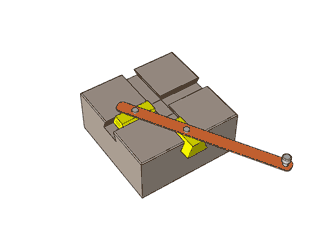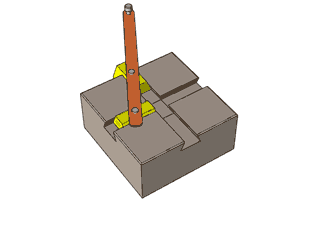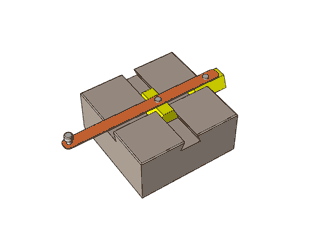
3: Sewing Machines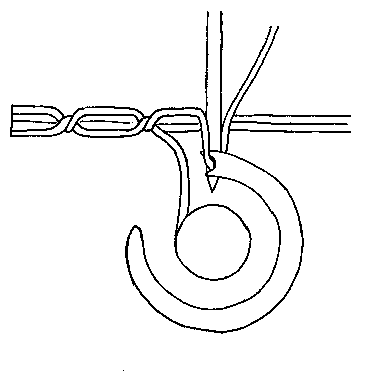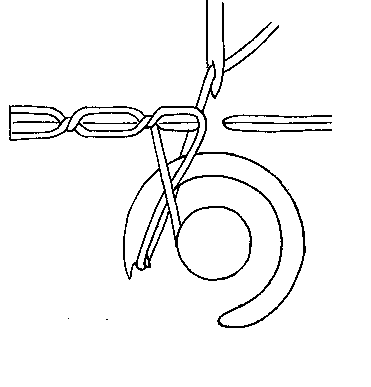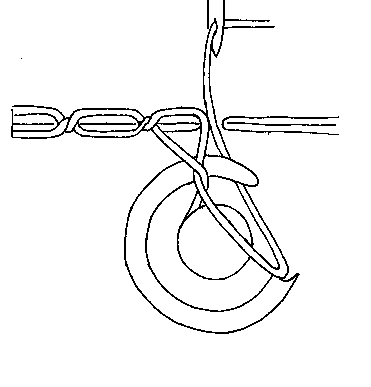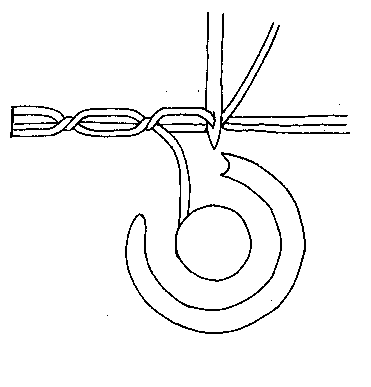
4: Malta Cross movement - second hand movement used to
control the clock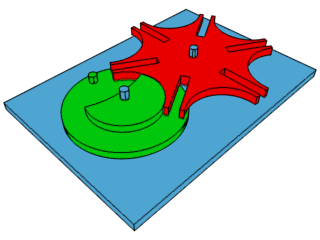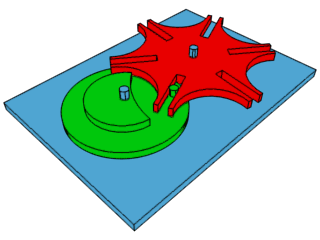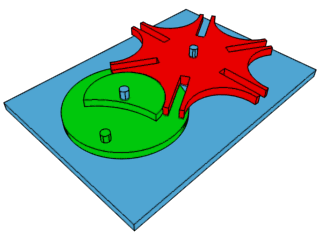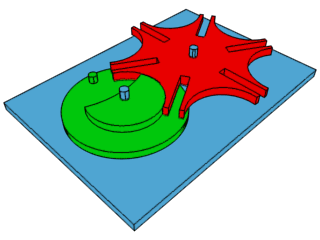
5: Auto Change file mechanism
6: Auto Constant Velocity Universal Joint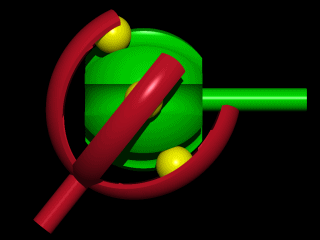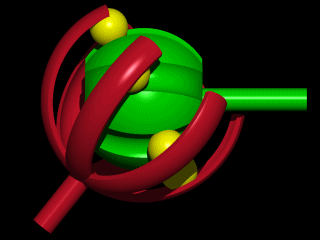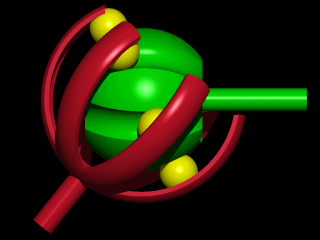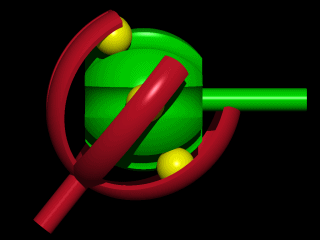
7: Gun Ammunition loading system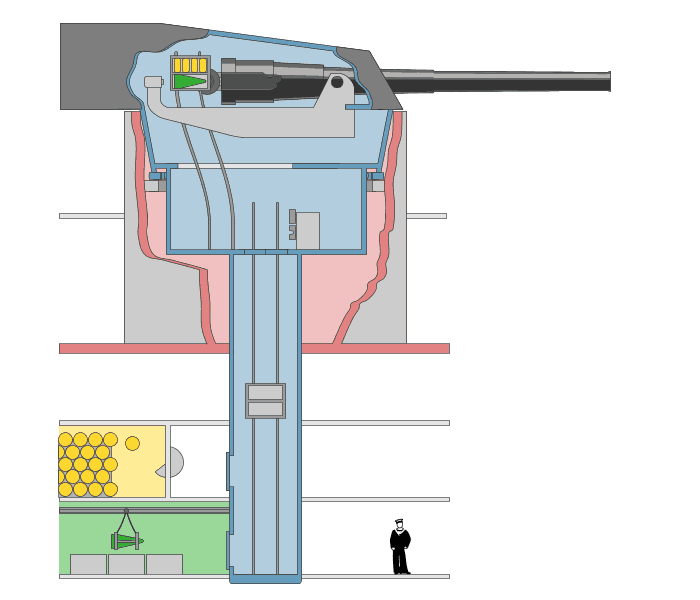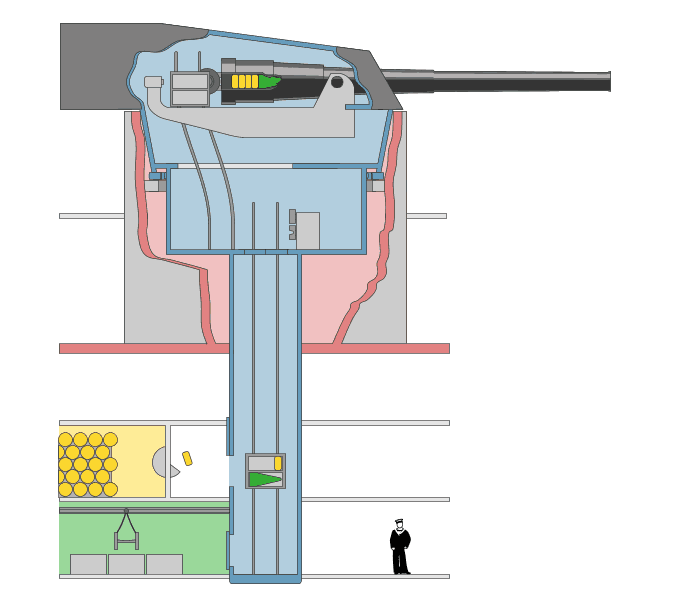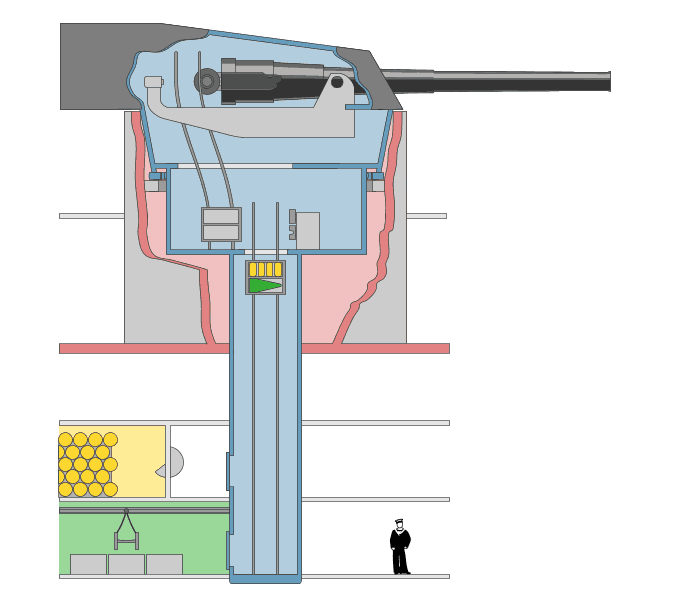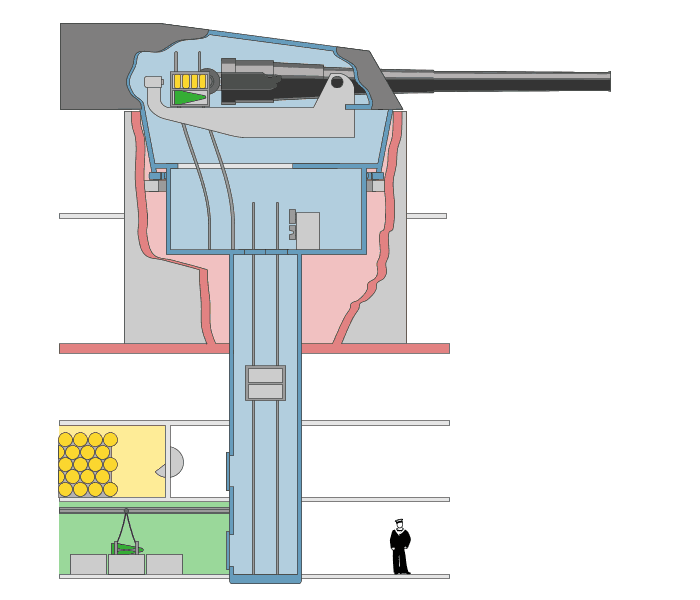
8: Rotary Engine - an internal combustion engine,
the heat rather than the piston movement into rotary movement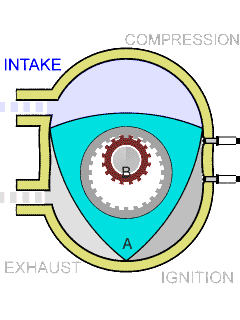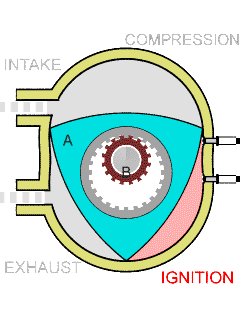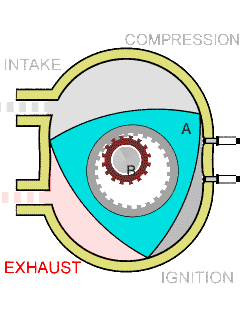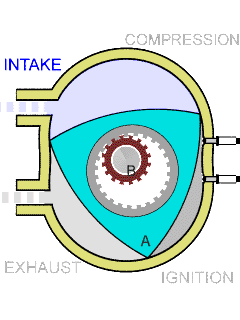
9: Engine - it's cylinders lined up side by side